深度学习笔记

提升自己对神经网络结构理解、代码复现的能力。

4月21日

1.AI地图

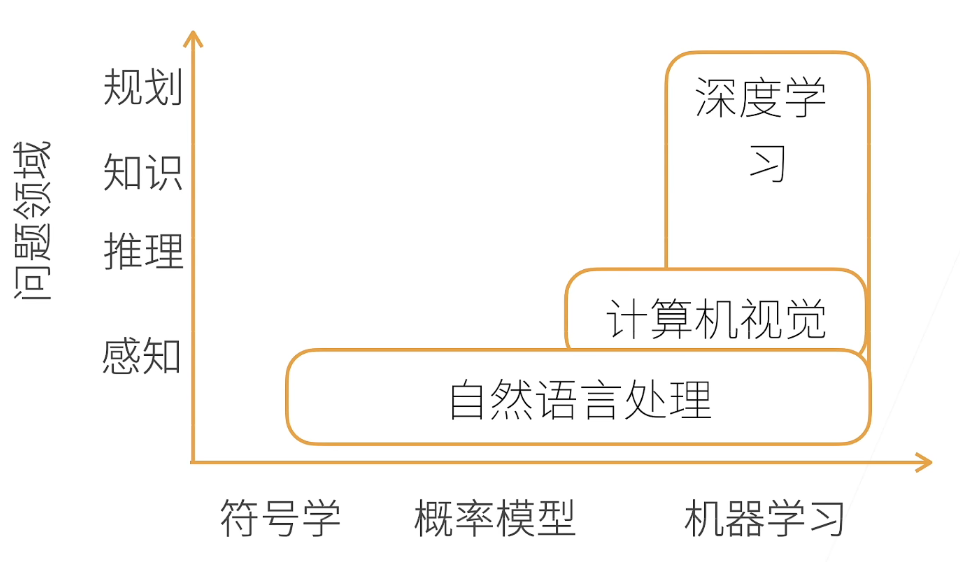
2.节省内存的方法

Y = X + Y (❌)
Z = X + Y (✔)
X += Y (✔)

3.多维矩阵

1）对于一个3维矩阵 shape=[2, 2, 3]，代码如下：

1	x = torch.arange(12).reshape(2, 2, 3)

可视化如下：

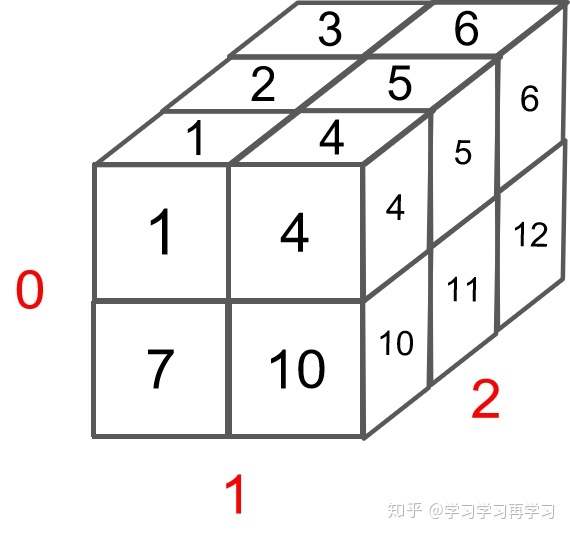
2）对于一个4维矩阵shape=[2,2,2,3]，代码如下：

1	y = torch.arange(1, 25).reshape(2, 2, 2, 3)

可视化如下：

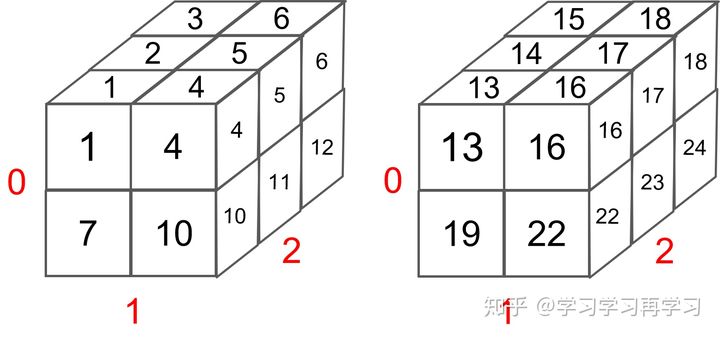
3）多维矩阵乘法

三维中，第一个值相等，后两维就是正常的矩阵相乘。

例：a：shape=[2, 2, 4]，b：shape=[2, 4, 3]相乘，输出shape=[2, 2, 3]。

四维中，前两维是矩阵排列，相乘的话保留前的最大值。后两维就是正常的矩阵相乘。

例：a：shape=[2,1,4,5]，b：shape=[1,1,5,4]相乘，输出的结果中，前两维保留的是[2,1]，最终结果shape= [2,1,4,4]。

4）多维矩阵转置

shape=[2,2,4] 转置之后为 shape=[4, 2, 2]

4月22日

4.矩阵计算

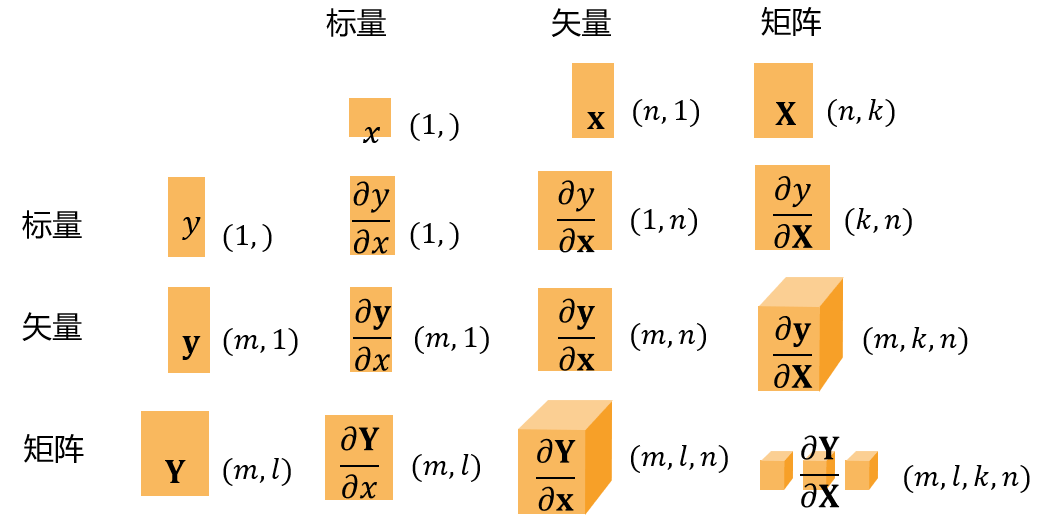
5.在深度学习中，我们“训练”模型，不断更新它们，使它们在看到越来越多的数据时变得越来越好。通常情况下，变得更好意味着最小化一个损失函数（loss function），即一个衡量“我们的模型有多糟糕”这个问题的分数。最终，我们真正关心的是生成一个模型，它能够在从未见过的数据上表现良好。但“训练”模型只能将模型与我们实际能看到的数据相拟合。因此，我们可以将拟合模型的任务分解为两个关键问题：

优化（optimization）：用模型拟合观测数据的过程；
泛化（generalization）：数学原理和实践者的智慧，能够指导我们生成出有效性超出用于训练的数据集本身的模型。

微分可以应用于深度学习中的优化问题，梯度是一个向量，其分量是多变量函数相对于其所有变量的偏导数。

4月23日

6.使用nn.Module实现一个线性回归模型

import torch
import torch.nn as nn

class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()
        self.linear = nn.Linear(n_feature, 1)
    # forward 定义前向传播
    def forward(self, x):
        y = self.linear(x)
        return y

num_inputs = 2
net = LinearNet(num_inputs)
print(net) # 使用print可以打印出网络的结构

4月24日

7.优化算法

梯度下降通过不断沿着反梯度方向更新参数求解
小批量随机梯度下降使深度学习默认的求解算法
两个重要的超参数使批量大小和学习率

8.线性回归简洁实现

1）生成自定义数据集

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)   # 生成1000个样本

2）读取数据集

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    # 布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)
# 使用iter构造Python迭代器，并使用next从迭代器中获取第一项
next(iter(data_iter))

3）定义模型

# nn是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

# 初始化模型参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

4）定义损失函数

1	loss = nn.MSELoss() # 默认情况下，它返回所有样本损失的平均值。

5）定义优化算法

1 2	# 采用小批量随机梯度下降算法 trainer = torch.optim.SGD(net.parameters(), lr=0.03)

6）训练

num_epochs = 3                                # 迭代周期

# 在每个迭代周期里，我们将完整遍历一次数据集（train_data）， 不停地从中获取一个小批量的输入和相应的标签。
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)                   # 通过调用net(X)生成预测并计算损失l（前向传播）
        trainer.zero_grad()
        l.backward()                          # 通过进行反向传播来计算梯度
        trainer.step()                        # 通过调用优化器来更新模型参数
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

7）* 比较误差

# 要访问参数，我们首先从net访问所需的层，然后读取该层的权重和偏置
w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

9.Softmax回归

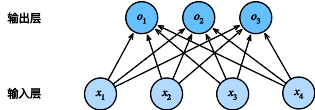
Softmax回归是一个多类分类模型
使用Softmax操作子得到每个类的预测置信度
使用交叉熵来衡量预测和标号的区别

Softmax回归的简洁实现

1）导入Fashion-MNIST数据集

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2）定义模型

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10)) # softmax回归的输出层是一个全连接层(10个输出)

# 初始化权重
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

3）定义损失函数

1	loss = nn.CrossEntropyLoss(reduction='none')

4）定义优化算法

1	trainer = torch.optim.SGD(net.parameters(), lr=0.1)

5）训练

1 2	num_epochs = 10 d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

4月25日

10.多层感知机（MLP）

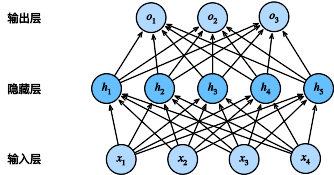
多层感知机使用隐藏层和激活函数来得到非线性模型
常用的激活函数有

1）Sigmoid

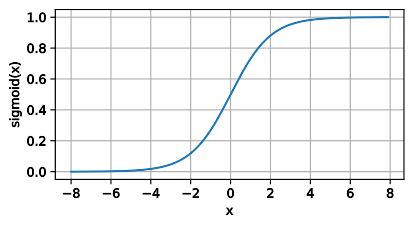
2）ReLU（使用较多）

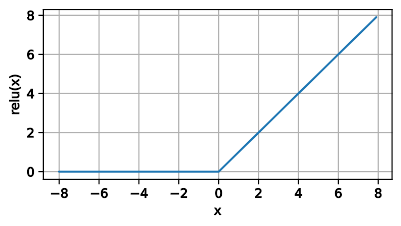
3）tanh
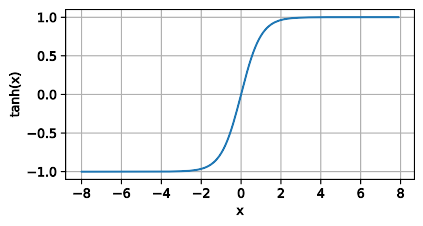
使用Softmax来处理多类分类
超参数为隐藏层数，和各个隐藏层大小

多层感知机简洁实现

1）导入Fashion-MNIST数据集

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
lr = 0.1
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2 ）定义模型

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),    # 定义隐藏层
                    nn.ReLU(),              # 定义激活函数
                    nn.Linear(256, 10))     # 定义输出层

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

3）训练

num_epochs = 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

4月26日

11.权重衰减

权重衰退通过$L_2$正则项使得模型参数不会过大，从而控制模型复杂度
正则项权重（wd）是控制模型复杂度的超参数

原损失函数：

$L(\mathbf{w}, b) = \frac{1}{n}\sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2.$

$L_2$正则化回归的小批量随机梯度下降：

$L(\mathbf{w}, b) + \frac{\lambda}{2} |\mathbf{w}|^2,$

参数更新如下：

$\begin{aligned} \mathbf{w} & \leftarrow \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned}$

$L_2$正则化权重衰减简洁实现：

在实例化优化器时直接通过weight_decay指定weight decay超参数。默认情况下，PyTorch同时衰减权重和偏移。这里我们只为权重设置了weight_decay，所以偏置参数 $b$ 不会衰减。

def train_concise(wd):                                   # 定义训练函数
    net = nn.Sequential(nn.Linear(num_inputs, 1))
    for param in net.parameters():
        param.data.normal_()
    loss = nn.MSELoss(reduction='none')
    num_epochs, lr = 100, 0.003
    # 偏置参数b没有衰减
    trainer = torch.optim.SGD([
        {"params":net[0].weight,'weight_decay': wd},     # 权重衰减（参数为wd,一般取e-3）
        {"params":net[0].bias}], lr=lr)
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.mean().backward()
            trainer.step()
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1,
                         (d2l.evaluate_loss(net, train_iter, loss),
                          d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数：', net[0].weight.norm().item())

12.Dropout(暂退法)

暂退法将一些输出项随机置0来控制模型复杂度
常作用在多层感知机的隐藏层输出上
暂退概率是控制模型复杂度的超参数

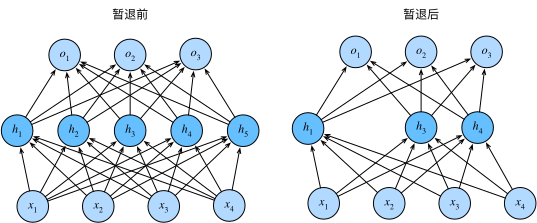
在标准暂退法正则化中，通过按保留（未丢弃）的节点的分数进行规范化来消除每一层的偏差。换言之，每个中间活性值$h$以暂退概率$p$由随机变量$h’$替换，如下所示：

$\begin{aligned} h' = \begin{cases} 0 & \text{ 概率为 } p \ \\ \frac{h}{1-p} & \text{ 其他情况} \end{cases} \end{aligned}$

根据此模型的设计，其期望值保持不变，即$E[h’] = h$。

Dropout简洁实现：

在定义网络时，只需在每个全连接层之后添加一个Dropout层，将暂退概率作为唯一的参数传递给它的构造函数。在训练时，Dropout层将根据指定的暂退概率随机丢弃上一层的输出（相当于下一层的输入）。在测试时，Dropout层仅传递数据。

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),                    # 第一个隐藏层
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1 = 0.2),
        nn.Linear(256, 256),                    # 第二个隐藏层
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2 = 0.5),
        nn.Linear(256, 10))                     # 输出层

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

13.合理的权重初始值（服从正态分布，均值为0，方差为一个常数）和激活函数的选取可以提升数值稳定性。

4月27日—4月28日

Kaggle竞赛——California房价预测

notebook链接：

https://www.kaggle.com/code/mikeypan0721/california-house-price-mlp

4月29日

14.卷积神经网络

1）多层感知机适合处理表格数据，但对于高维感知数据，卷积神经网络更加实用。

2）卷积神经网络（convolutional neural networks，CNN）是机器学习利用自然图像中一些已知结构的创造性方法。

3）从全连接层——>卷积

$\begin{aligned} \left[\mathbf{H}\right]_{i, j} &= [\mathbf{U}]_{i, j} + \sum_k \sum_l[\mathsf{W}]_{i, j, k, l} [\mathbf{X}]_{k, l}\ \\ &= [\mathbf{U}]_{i, j} + \sum_a \sum_b [\mathsf{V}]_{i, j, a, b} [\mathbf{X}]_{i+a, j+b}.\end{aligned}$

4）平移不变性

平移不变性意味着检测对象在输入$\mathbf{X}$中的平移，应该仅导致隐藏表示$\mathbf{H}$中的平移。也就是说，$\mathsf{V}$和$\mathbf{U}$实际上不依赖于$(i, j)$的值，即$[\mathsf{V}]_{i, j, a, b} = [\mathbf{V}]_{a, b}$。并且$\mathbf{U}$是一个常数，比如$u$。因此，我们可以简化$\mathbf{H}$定义为：

$[\mathbf{H}]_{i, j} = u + \sum_a\sum_b [\mathbf{V}]_{a, b} [\mathbf{X}]_{i+a, j+b}.$

这就是卷积（convolution）。我们是在使用系数$[\mathbf{V}]_{a, b}$对位置$(i, j)$附近的像素$(i+a, j+b)$进行加权得到$[\mathbf{H}]_{i, j}$。注意，$[\mathbf{V}]_{a, b}$的系数比$[\mathsf{V}]_{i, j, a, b}$少很多，因为前者不再依赖于图像中的位置。

5）局部性

为了收集用来训练参数$[\mathbf{H}]_{i, j}$的相关信息，我们不应偏离到距$(i, j)$很远的地方。这意味着在$|a|> \Delta$或$|b| > \Delta$的范围之外，我们可以设置$[\mathbf{V}]_{a, b} = 0$。因此，我们可以将$[\mathbf{H}]_{i, j}$重写为:

$[\mathbf{H}]_{i, j} = u + \sum_{a = -\Delta}^{\Delta} \sum_{b = -\Delta}^{\Delta} [\mathbf{V}]_{a, b} [\mathbf{X}]_{i+a, j+b}.$

这是一个卷积层（convolutional layer），而卷积神经网络是包含卷积层的一类特殊的神经网络。

6）卷积层

卷积层将输入和核矩阵进行交叉相关，加上偏移后得到输出
核矩阵和偏移是可学习的参数
核矩阵的大小是超参数

卷积网络代码实现：

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):  #@save
    """计算二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

# 定义卷积层
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

# 学习卷积核
# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')
        
conv2d.weight.data.reshape((1, 2))

7）填充与步幅

填充和步幅是卷积层的超参数
填充在输入周围添加额外的行/列，来控制输出形状的减少量

步幅是每次滑动核窗口时的行/列的步长，可以成倍的减少输出形状

代码实现：

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)

conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)

conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))

5月2日

8）多输入多输出通道

输出通道数是卷积层的超参数
每个输入通道有独立的二维卷积核，所有通道结果相加得到一个输出通道结果
每个输出通道有独立的三维卷积核

import torch
from d2l import torch as d2l

# 多输入通道互相关运算
def corr2d_multi_in(X, K):
    # 先遍历“X”和“K”的第0个维度（通道维度），再把它们加在一起
    return sum(d2l.corr2d(x, k) for x, k in zip(X, K))

X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)

# 多输出通道互相关函数
def corr2d_multi_in_out(X, K):
    # 迭代“K”的第0个维度，每次都对输入“X”执行互相关运算。
    # 最后将所有结果都叠加在一起
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

# 通过将核张量K与K+1（K中每个元素加1）和K+2连接起来，构造了一个具有3个输出通道的卷积核。
K = torch.stack((K, K + 1, K + 2), 0)
K.shape

# 对输入张量X与卷积核张量K执行互相关运算。现在的输出包含3个通道，第一个通道的结果与先前输入张量X和多输入单输出通道的结果一致
corr2d_multi_in_out(X, K)

# 使用全连接层实现1×1卷积，首先需要对输入和输出的数据形状进行调整。
def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
    # 全连接层中的矩阵乘法
    Y = np.dot(K, X)
    return Y.reshape((c_o, h, w))

# 当执行1×1卷积运算时，上述函数相当于先前实现的互相关函数corr2d_multi_in_out。让我们用一些样本数据来验证这一点。
X = np.random.normal(0, 1, (3, 3, 3))
K = np.random.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(np.abs(Y1 - Y2).sum()) < 1e-6

9）池化层

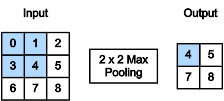
池化层返回窗口中最大或平均值
缓解卷积层位置的敏感性
同样有窗口的大小、填充和步幅作为超参数

import torch
from torch import nn
from d2l import torch as d2l

def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))

pool2d(X, (2, 2), 'avg')

# 填充与步幅
X = np.arange(16, dtype=np.float32).reshape((1, 1, 4, 4))
X

# 默认情况下，深度学习框架中的步幅与池化窗口的大小相同。 因此，如果我们使用形状为(3, 3)的池化窗口，那么默认情况下，我们得到的步幅形状为(3, 3)
pool2d = nn.MaxPool2d(3)
pool2d(X)

# 手动设定填充和步幅
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

# 手动设定一个任意大小的矩形池化窗口，并分别设定填充和步幅的高度和宽度
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)

# 多通道
# 在处理多通道输入数据时，汇聚层在每个输入通道上单独运算，而不是像卷积层一样在通道上对输入进行汇总。 这意味着汇聚层的输出通道数与输入通道数相同。 下面，我们将在通道维度上连结张量X和X + 1，以构建具有2个通道的输入。
X = torch.cat((X, X + 1), 1)
X

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

5月3日

15.LeNet

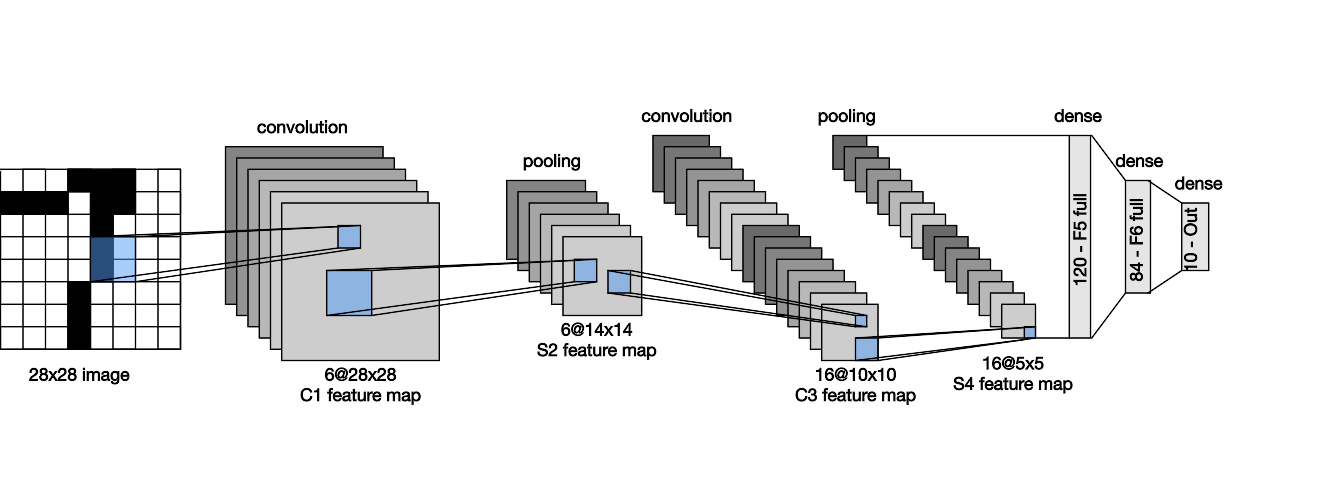
LeNet是早期成功的神经网络
先使用卷积层来学习图片空间信息
然后使用全连接层来转换到类别空间

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

# 显示输出
X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape: \t',X.shape)
 
# 模型训练
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使用GPU计算模型在数据集上的精度"""
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                # BERT微调所需的（之后将介绍）
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')
    
lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

5月4日

16.AlexNet

相当于更大更深的LeNet，10x参数个数，260x计算复杂度
新加入了丢弃法、ReLU、最大池化层和数据增强

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    # 这里，我们使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

# 观察每一层输出
X = torch.randn(1, 1, 224, 224)
for layer in net:
    X=layer(X)
    print(layer.__class__.__name__,'output shape:\t',X.shape)
    
# 读取数据集
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)

# 训练
lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

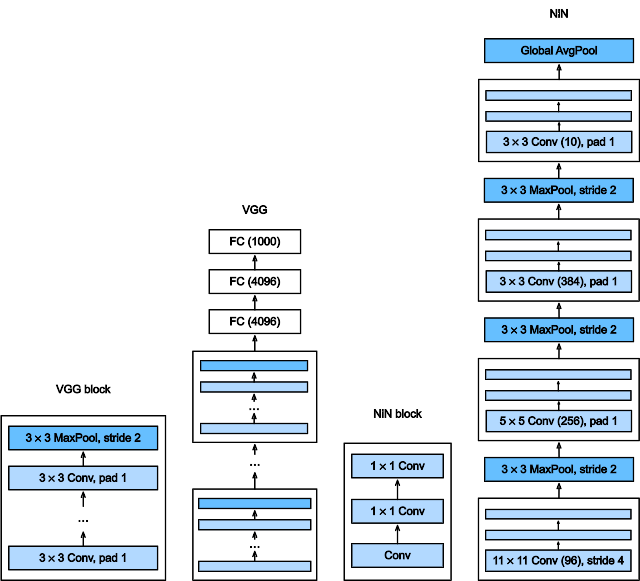
17.VGG

VGG使用可重复的卷积块来构建深度卷积神经网络
不同的卷积块个数和超参数可以得到不同复杂度的变种

import torch
from torch import nn
from d2l import torch as d2l

# 定义VGG块
def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))

# 定义神经网络
def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    # 卷积层部分
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(
        *conv_blks, nn.Flatten(),
        # 全连接层部分
        nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10))

net = vgg(conv_arch)

# 观察每一层输出
X = torch.randn(size=(1, 1, 224, 224))
for blk in net:
    X = blk(X)
    print(blk.__class__.__name__,'output shape:\t',X.shape)
    
# 训练
ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

18.NiN

NiN使用卷积层加两个1x1卷积层，后者的作用相当于全连接层，对每个像素增加了非线性性
NiN使用全局平均池化层来替代VGG和AlexNet中的全连接层，优点是不容易过拟合，更少的参数个数

import torch
from torch import nn
from d2l import torch as d2l

# 定义NiN块
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

# 定义神经网络
net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

# 显示每一层输出
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)
    
# 训练
lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

5月5日

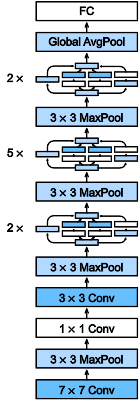
19.GoogLeNet

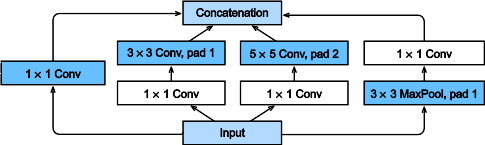
在GoogLeNet中，基本的卷积块被称为 Inception块（Inception block）。

Inception块用4条有不同超参数的卷积层和池化层来抽取不同的信息，优点是模型参数小，计算复杂度低
GoogLeNet使用了9个Inception块，是第一个达到上百层的网络

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

# 定义Inception块
class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)
    
# 定义GoogLeNet模型
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1,1)),
                   nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

# 显示每一次输出
X = torch.rand(size=(1, 1, 96, 96))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

# 训练模型
lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

20.批量归一化

批量归一化固定小批量中的均值和方差，然后学习出适合的偏移和缩放
可以加速收敛速度，但一般不改变模型精度

$\begin{aligned} \hat{\boldsymbol{\mu}}_\mathcal{B} &= \frac{1}{|\mathcal{B}|} \sum_{\mathbf{x} \in \mathcal{B}} \mathbf{x},\ \\\hat{\boldsymbol{\sigma}}_\mathcal{B}^2 &= \frac{1}{|\mathcal{B}|} \sum_{\mathbf{x} \in \mathcal{B}} (\mathbf{x} - \hat{\boldsymbol{\mu}}_{\mathcal{B}})^2 + \epsilon.\end{aligned}$ $\mathrm{BN}(\mathbf{x}) = \boldsymbol{\gamma} \odot \frac{\mathbf{x} - \hat{\boldsymbol{\mu}}_\mathcal{B}}{\hat{\boldsymbol{\sigma}}_\mathcal{B}} + \boldsymbol{\beta}.$

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
    nn.Linear(84, 10))

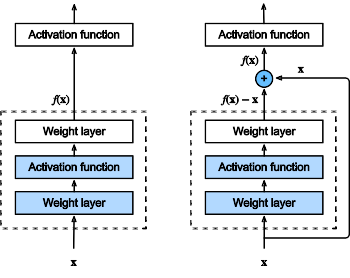
21.ResNet

残差块使得很深的网络更加容易训练
残差网络对随后的深层神经网络设计产生了深远影响，无论是卷积类网络还是全连接类网络

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

# 定义残差块
class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

# 查看输入和输出一致的情况
blk = Residual(3,3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape

# 增加输出通道数的同时，减半输出的高和宽
blk = Residual(3,6, use_1x1conv=True, strides=2)
blk(X).shape

# 定义ResNet模型
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels,
                                use_1x1conv=True, strides=2))
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk

# 在ResNet加入所有残差块，这里每个模块使用2个残差块。
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

# 与GoogLeNet一样，在ResNet中加入全局平均汇聚层，以及全连接层输出
net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1,1)),
                    nn.Flatten(), nn.Linear(512, 10))

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)
    
# 训练
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

5月6日—5月7日

Kaggle竞赛——Classify Leaves

notebook链接：

https://www.kaggle.com/code/charlesyyun/7th-resnest-resnext-densenet-0-98840

5月8日

22.数据增强

数据增强通过变形数据来获得多样性从而使得模型泛化性能更好
常见图片增强包括翻转、切割、变色

train_transform = transforms.Compose([
    # 随机裁剪图像，所得图像为原始面积的0.08到1之间，高宽比在3/4和4/3之间。
    # 然后，缩放图像以创建224 x 224的新图像
    transforms.RandomResizedCrop(224, scale=(0.08, 1.0), ratio=(3.0 / 4.0, 4.0 / 3.0)),
    # 随机水平翻转
    transforms.RandomHorizontalFlip(),
    # 随机更改亮度，对比度和饱和度
    transforms.ColorJitter(brightness=0.4, contrast=0.4, saturation=0.4),
    # 添加随机噪声
    transforms.ToTensor(),
    # 标准化图像的每个通道
    transforms.Normalize([0.485, 0.456, 0.406],[0.229, 0.224, 0.225])])
val_test_transform = transforms.Compose([
    transforms.Resize(256),
    # 从图像中心裁切224x224大小的图片
    transforms.CenterCrop(224),
    transforms.ToTensor(),
    transforms.Normalize([0.485, 0.456, 0.406],[0.229, 0.224, 0.225])])

23.微调（预训练）

微调通过使用在大数据上得到的预训练好的模型来初始化模型权重来完成提升精度
预训练模型质量很重要
微调通常速度更快、精度更高

# ResNeSt模型
def resnest_model(num_classes, feature_extract = False):
    model_ft = resnest50(pretrained=True)
    set_parameter_requires_grad(model_ft, feature_extract)
    num_ftrs = model_ft.fc.in_features
    model_ft.fc = nn.Sequential(nn.Linear(num_ftrs, num_classes))

    return model_ft

6月11日

从今天开始看循环神经网络

https://zh.d2l.ai/chapter_recurrent-neural-networks/index.html

6月16日

从今天开始看Transformers

https://datawhalechina.github.io/learn-nlp-with-transformers